Dual Contouring
API function: algo.dualContouring
The Dual Contouring algorithm creates a new mesh representing the selected occurrences. This is built using an improved version of the Dual Contouring algorithm, built on an octree.
The algorithm
The dual contouring is in essence quite similar to the marching cubes. It works on voxels (in our case in an octree). However, it is the dual of the marching cubes (though its name) as it creates a vertex per voxel, instead of vertices on the edges of the voxels.
The improvements on the base method are stability related, and allow the filtering of a given size of elements, meaning that some geometry will be created in concavities when they are smaller than the filtering size. It also means as a side effect that models closer than this filtering size will be merged (see examples below).
Other retopology methods are proxy mesh (based on marching cubes) and retopologize (based on instant meshes).
This example shows a model before and after processing:
 From left to right: Dual contouring (1K triangles), LOD0 (25K triangles), Proxy Mesh (1K triangles).
From left to right: Dual contouring (1K triangles), LOD0 (25K triangles), Proxy Mesh (1K triangles).
Tip
This function does not compute nor uses normals. This means that after it, you might want to orient the polygons and create some normals before baking onto the model. See scrit below for a usage example.
Parameters
Filtering size
This is the size (in millimeters) used for filtering the recontruction. This means that the algorithm will fill-in cavities and holes smaller than this size and will concatenate parts or occurrences that are closer than the filtering size even when they are not originally connected.
This filtering size corresponds to the octree depth at which the algorithm stops its descent.
Here is an example of the effect of filtering size. Other parameters are voxel size = 0.25 and tolerance = 10:

Tip
The filtering size must be a multiple of 2 of the voxel size.
Voxel size
This is the size (in millimeters) used for the reconstruction. It corresponds to the minimum size the triangles/quadrangles are allowed to have.
This size corresponds to the maximum octree depth that will be used in the algorithm, thus fixing the minimum size of the created geometry.
Tolerance
The new points are created following quadric errors. This tolerance is the maximum error authorized for a quadric. It will allow the grouping of octree nodes as long as the new encompassing quadric error is below the tolerance.
This means that a higher value will result in a more approximative geometry, but with less triangles, while a lower value will create more triangles (limited at the maximum depth fixed by the voxel size). This value needs specific tuning for every model.
Tip
A negative value will result in no simplification (no voxel groupings), so polygons size will match the voxel size or the filtering size depending on where they are on the models.
This example shows the effect of the tolerance parameter:

Same size on all axis
When true, it will use the maximum size on every axis and create a base node for the octree that will be a cube of this size. Otherwise, a parallelepiped of the dimension of the AABB will be used, which can lead to more finer recontruction on the narrower sides.
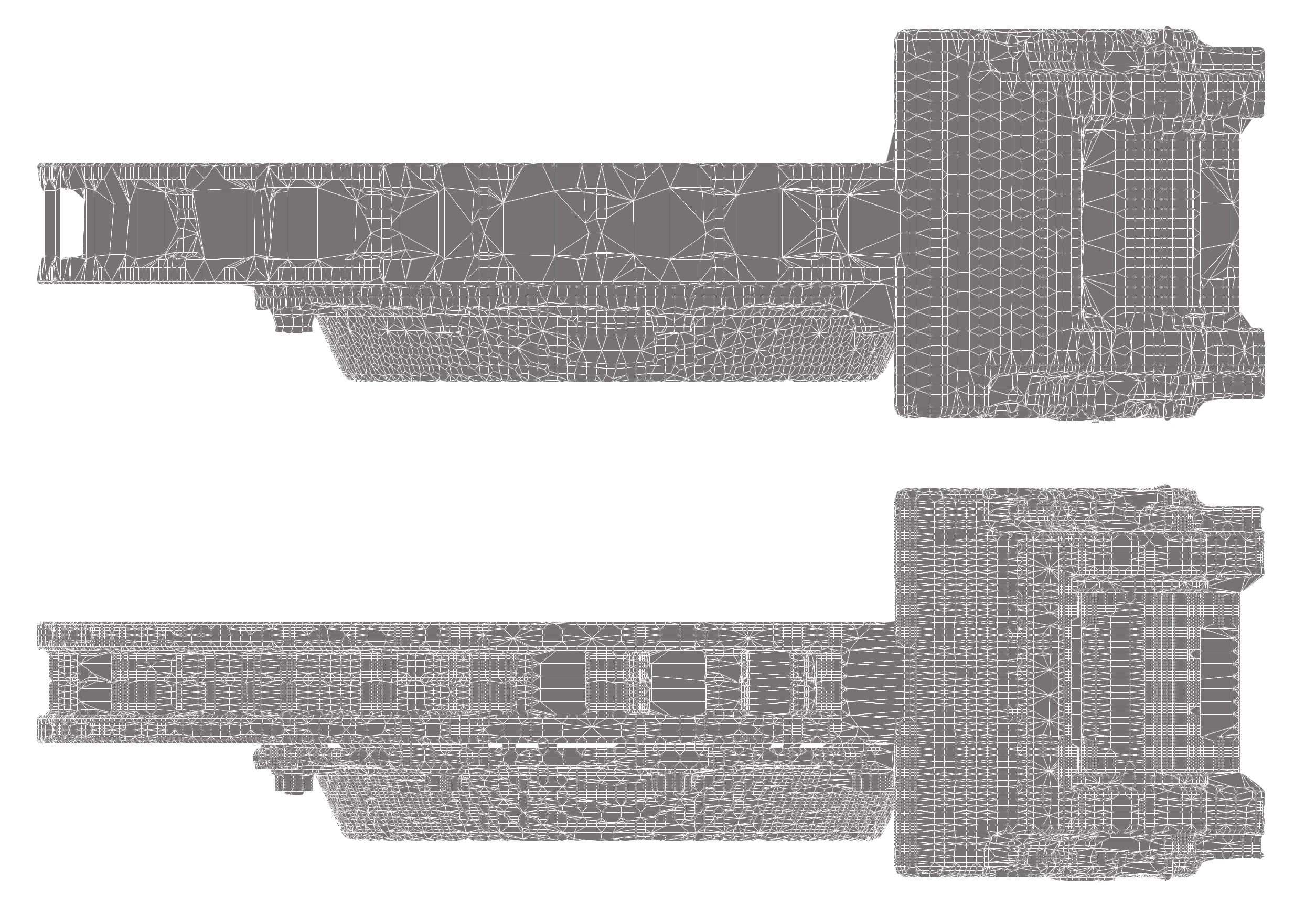
On top, sameSizeOnAllAxis checked, on the bottom, unchecked:
Usage example
Here is an example of a script creating a dual contour with normals (but without baking):
root = pxz.scene.getRoot()
dc = pxz.algo.dualContouring(occurrences=root,filteringSize=200.0,voxelSize=50.0,tolerance=0.001,sameSizeOnAllAxis=True)
pxz.algo.orientPolygonFaces(occurrences=[dc],makeOrientable=True,useArea=True,orientStrategy=1)
pxz.algo.createNormals(occurrences=[dc],override=True,useAreaWeighting=True)